| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | |||
| 5 | 6 | 7 | 8 | 9 | 10 | 11 |
| 12 | 13 | 14 | 15 | 16 | 17 | 18 |
| 19 | 20 | 21 | 22 | 23 | 24 | 25 |
| 26 | 27 | 28 | 29 | 30 | 31 |
- 깃
- Vue3
- TiL
- 프로그래머스
- 개발프로젝트
- greedy
- 1일1커밋
- 개발회고록
- SSAFY
- python알고리즘
- TMI일상
- Python
- jupyternotebook
- SSAFY 5기
- vue에러
- Bootstrap-Vue
- 회고록
- error
- Vue.js
- 회고
- replit
- 싸피
- 개발
- 프로젝트
- 싸피 프로젝트
- 개발자
- SSAFY 2학기
- 알고리즘
- Git
- PJT
- Today
- Total
def(aluu):
차근차근알고1 - 피보나치로 재귀에서 DP맛보기(메모이제이션)까지 (python) 본문
목차
1. 재귀함수(Recursive Function)란?
재귀함수 호출의 리턴과정
2. 피보나치로 보는 재귀함수
피보나치수열 재귀 코드 (python)
메모이제이션으로 구현하기
메모이제이션으로 구현한 피보나치수열 코드 (python
3. 재귀함수를 써야하는 이유
알고리즘 공부한지 어언 2년.. 하지만 매번 알고리즘 공부를 할 때마다 새롭다...⛧
또 매번 기억이 안 나니까 처음부터 해야지 하다보니 실력이 앞에서만 맴돌고 있다. 수 1 집합 수십 번 보던 사람 나야 나!

그래서 이번에는 알고리즘 꾸준히 해서 절대 다시 돌아오지 않는다는 마음으로 공부해보려고 한다.
간단하게.. 최대한 간단하게...
첫 번째는 주인공은 바로바로 재귀함수!
이유는 글쎄.. 그냥 알고리즘 배울 때 초반에 이거 배웠던 것 같아서?
1. 재귀함수(Recursive Function)란?
자기 자신을 호출하는 함수이다.
한마디로 정의하면 이런데, 풀어서 설명하자면 A함수를 실행하면서 A와 똑같은 A' 함수를 불러오고(아마 인자가 달라지겠지) 그러면 또 그 A' 함수에서 A''함수를 불러오고... 의 반복이다. '이러면 언제 끝나는 거야!' 하고 생각할 수 있는데, 그래서 재귀함수를 쓸 때는 반드시 탈출 조건이 있어야 stack overflow를 방지할 수 있다!
재귀함수의 호출 및 리턴 과정
함수 호출의 원리 및 재귀 호출을 참고했다. (이미지도 여기서 들고 왔다)

재귀함수의 경우 코드를 진행하다가 재귀함수를 호출하면 재귀함수가 불러온다. 계속 같은 함수가 불러지는 이 과정이 복잡하게 느껴질 수도 있지만 사실 일반적인 함수의 호출과 별 다를 것은 없다.

함수 A 안에 함수 B가 있고 함수B 안에 함수C가 있는 경우를 생각한다. 이 때 함수C가 끝나면 함수 B의 다음 라인으로 넘어갈 것이고, 함수B가 다 불러왔으면 함수 A로 넘어갈 것이다. 함수 A가 끝나면 main 함수로 넘어가겠지?

다시 재귀함수를 보면 똑같이 생긴 함수이지만 새로운 메모리 공간이 생성된다. 그래서 같은 A함수가 아니라 A', A''는 다른 함수로 보면 일반적인 함수 호출과 다를게 없다. 하지만 아무튼 똑같이 생긴 함수이므로 언젠가는 그 함수에서 탈출하는 날이 와야한다. 그래서 탈출 조건이 필요하다. 코드 예시를 보면 알겠지만, 재귀함수는 탈출조건이 있어서 마지막 함수에서 다시 돌아올 수 있다! (있어야만 한다...도르마무 된다구..)

2. 피보나치로 보는 재귀함수
재귀함수를 코드로 구현하기 위해서 피보나치 수열을 구현하려고 한다.
어릴 때 수학귀신이라는 책에서 봤던 피보나치가 여기 나온다...! 다들 수학귀신 알겠지? (나이 많은 거 이렇게 들키나..?)

피보나치란 첫째, 둘째 항이 1이고, 그 뒤의 모든 항은 바로 앞 두 항의 합인 수열이다.

이렇게 나오게 된다. 그러면 파이썬으로는 어떻게 코드를 짤 수 있을까?
피보나치수열 재귀 코드 (python)
def fibo(n):
if n <= 2: # 탈출 조건
return 1
else:
return fibo(n-1) + fibo(n-2) # 재귀 호출
print(fibo(10)) # 55이렇게 함수 안에 자기 자신의 함수를 가진 재귀함수를 짤 수 있다.
처음 재귀함수를 접하면 이 함수가 와닿지 않을까 봐 그림을 그려봤는데...

함수 안에 자기 자신과 같은 함수라고 당황하지 않고, 자신과 똑같이 생겼지만 다른 함수를 불러온다고 생각해야 한다!
그리고 이렇게 리턴값들을 모아 모아 최종 값이 나오게 된다!
메모이제이션으로 구현하기
위의 방법대로 했을 때 문제는 느리다는 것이다. (재귀함수는 느려!) 이것을 더 빠른 재귀함수로 만들어보자.
바로 메모이제이션을 쓰는 것이다!
💡 메모이제이션: 컴퓨터 프로그램이 동일한 계산을 반복해야 할 때, 이전에 계산한 값을 메모리에 저장함으로써 동일한 계산의 반복 수행을 제거하여 프로그램 실행 속도를 빠르게 하는 기술
쉽게 말하면

위의 그림에서 이렇게 반복되는 연산들이 있다. 이런 것들을 없애주는 것이다.
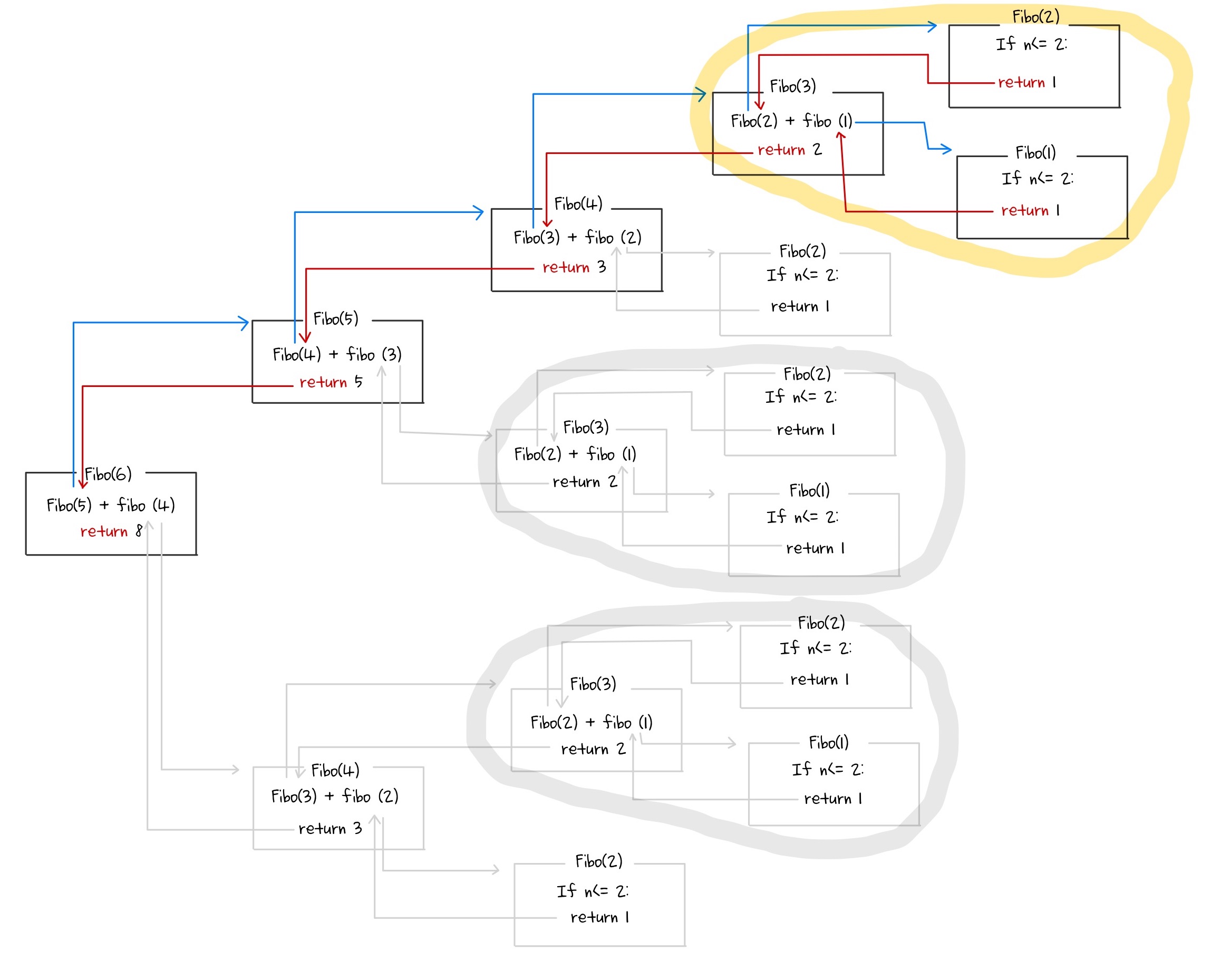
동그라미 친 것뿐 아니라 반복되는 연산들을 모두 없애면 이렇다! 간단해지겠지?
이걸 DP, 다이내믹 프로그래밍(동적계획법)라고도 한다. 정확하게 말하면 메모이제이션은 DP의 Bottom-up 방식인데...
사실 이거 방금 알았다... 그래서 바로 내일 DP에 대해서 써보겠다...Ꙭ̯
어쩌다가 재귀를 하려고 했는데 DP까지 흘러가고 있는 거야. 거의 내 블로그 진돌 유튜브 라이브 방송.

아무튼 메모이제이션 ⊂ DP(동적계획법)만 기억해 두고 넘어가자!
메모이제이션으로 구현한 피보나치수열 코드 (python)
그래서 넘어오면 이제 메모이제이션을 적용한 피보나치수열의 재귀함수 코드를 짜볼 거다.
dic = {1:1, 2:1}
def fib_memoization(n):
if n in dic: # 이미 fib_memoization(n)이 계산되었으면 그 값을 그대로 return
return dic[n]
# fib_memoization(n)이 계산되지 않았을 때
dic[n] = fib_memoization(n-1) + fib_memoization(n-2)
return dic[n]
print(fib_memoization(10)) # 55이렇게 dictionary로 만들 수 있다. dictionary를 사용하는 이유는 n이 있는지 확인하는 편한 코드이기 때문이다.
사실 꼭 재귀함수를 써야 하는 것은 아니다.
def fib_memoization2(n):
lst = [0,1] # 배열에 피보나치 수열 값 저장
for i in range(2,n+1): # n번째 까지 연산
lst.append(lst[i-1] + lst[i-2])
return lst[n]
print(fib_memoization2(10)) # 55이렇게 처음부터 값을 저장해서 값을 쓴다고 생각할 수 있다. 이것도 이전에 계산한 값을 메모리에 저장하기 때문에 메모이제이션이다.
3. 재귀함수를 써야 하는 이유
사실 재귀함수를 배웠지만, 실제로 쓰는 상황이 되면 두통이 오기 시작한다.
하지만 배웠으니 써먹어야지!
그래서 재귀함수를 써야하는 이유를 꼭 쓰고 싶었다. (사실 이렇게 적어도 나중에 안 쓸 수도 있다.)
재귀함수는 큰 문제(Main problem)를 작은 문제(Sub problem)로 분할해야 하는 경우에 유리하다.
재귀적 사고 자체가 프로그래밍에서 중요하다고 하니 오늘 이렇게 공부한 게 의미는 있을 것 같다! ⍢⋆*
재귀함수는 가독성을 높여준다.
반복문으로 작성하는 것보다 간단하게 작성해서 가독성을 높여줄 수 있다. 하지만 재귀는 내가 이해해야 돼..
알고리즘에서 DFS, BFS 등을 재귀로 구현할 수 있다 (물론 재귀가 아닌 다른 방법도 있다)
또한 여러 정렬, 검색, 탐색 문제들을 재귀로 풀 수 있다.
대부분 재귀가 아닌 방법도 있어서 결국 다른 방법으로 풀곤 했었는데... 이제 재귀도 놓치지 않도록 노력.. 하겠다고 다짐!!
끝내면서... 다음부터는 절대로 이렇게 열심히 안 써야지.
고장난 아이패드로 그림까지 그린다고 고생했는데 읽으니까 순식간이야(ㅠ)

참고 링크
10분TV 함수 호출의 원리 및 재귀 호출
회고록 블로그 [공부필기] 재귀함수를 사용하는 이유
'알고리즘' 카테고리의 다른 글
| Replit 사용법 - Replit 시작과 Github 연결(잔디 에러)까지 for 알고리즘 공부 (0) | 2022.03.11 |
|---|

